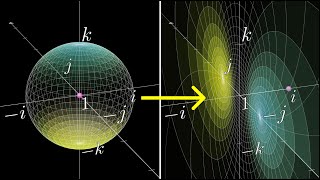
The geometry of "spin-vector addition" is shown. The spin-vectors exist in a spin-space that is equipped with three operations: scalar multiplication, inner product and addition. The addition of spin-vectors κ and ω results in another spin-vector κ + ω in the spin-space, which has its own flagpole and flag plane. Taking κ and ω as null vectors in the sphere of future null directions, the flagpole of κ is represented by a point (complex number) and the null flag of κ is represented as a point sufficiently close to κ that is used to assign a direction tangent to the sphere at κ.

The tails of the flagpoles of κ, ω and κ + ω are in a circle in the sphere of future null directions. The circumcircle of the triangle made by joining the tails of the three spin-vectors makes angles with the flagpoles and null planes. Meaning, the distance between κ and the center of the circle is equal to the distance between ω and the center. Also, the distance of the addition of κ and ω and the circle center is the same as the distance between κ and the center. For the circumcircle, we have three collinear points in the Argand complex plane. However, lines in the Argand plane become circles in sections of the three-dimensional sphere. The angle that the flagpoles of κ and ω make with the circle should be twice the argument of the inner product of the two spin-vectors (modulus 2π with a possible addition of π).

In an interesting way, the argument (phase) of the inner product of κ and ω is equal to half of the sum of the angles that the spin-vectors make with the circle, which is in turn equal to the angle that U and V make with each other minus π (also see the geometric descriptions of the inner product to construct U and V). In the case of spin-vector addition, the angles that the flag planes of κ, ω and κ + ω, each make with the circle are equal. But, be careful with determining the signs of the flag planes and the possible addition of π to the flag plane of κ + ω. For determining flag plane signs, see also Figure 1-21 in page 64 of Roger Penrose and Wolfgang Rindler, Spinors and Space-Time, Volume 1: Two-spinor calculus and relativistic fields, (1984).

https://iamazadi.github.io/Porta.jl/d...